Автор работы: ...
РАЗРАБАТЫВАЕМАЯ
ПРОГРАММА КУРСА АЛГЕБРЫ 7-9
кл.
Общая характеристика курса
В основе разрабатываемого курса лежат два основополагающих
понятия: математический язык и математическая модель.
С ними учащиеся в принципе знакомились и в начальной школе,
но если там эти понятия играли, в первую очередь, роль
средства, то теперь они становятся собственно объектами
исследования. Учащиеся знакомы с разными видами моделей.
Сейчас мы сосредотачиваемся на двух из них: геометрических
(линейных и площадных чертежах ) и знаковых (алгебраических)
моделях, с которыми связаны соответствующие языки. Причем
геометрический язык более наглядный и позволяет непосредственно
представлять отношения между числами и величинами; алгебраический
(знаковый) - более абстрактный, он является языком действий.
На стыке этих языков возникает координатный метод, который
и будет основным средством исследований на протяжении
всего курса, выступая в двух взаимосвязанных и взаимодополняющих
ролях: как средство описания геометрических объектов -
точечных множеств на прямой, на плоскости, а, впоследствии,
и в пространстве и как средство графической интерпретации
алгебраических объектов - уравнений, неравенств и, в первую
очередь, функциональных зависимостей.
Такой подход позволяет рассматривать эти основные виды
математических моделей не изолированно друг от друга,
а в тесной взаимосвязи, когда, например, уравнения и неравенства
(а также их системы) выступают как средство решения задач,
связанных с исследованием функций, а функциональные представления,
наоборот, положены в основу способов решения уравнений
и неравенств.
Рассмотрение указанных вопросов ведется от общего к частному.
Так, например, сначала вводятся общефункциональные представления
и ставятся общие задачи исследования функций, которые
затем конкретизируются для функций частного вида - линейной,
включая прямую пропорциональность (7 класс), квадратичной,
степенной функций, арифметической и геометрической прогрессий
(8, 9 классы).
Исследования, связанные с собственно алгебраическим языком,
составляют линию алгебраических преобразований, которая
выстраивается по тому же принципу - от общих понятий о
выражениях и их преобразовании к конкретным их видам -
целые рациональные выражения (7 класс), дробные рациональные
выражения, иррациональные выражения (8, 9 классы). При
этом линия алгебраических преобразований разворачивается
во времени таким образом, чтобы обеспечивать необходимым
инструментарием ведущую линию - линию математических моделей.
Перечисленные принципы позволят выстроить достаточно цельный
как по содержанию, так и по подходам курс.
Учителя и учащиеся постепенно по ходу разработки курса
будут обеспечиваться необходимым учебно-методическим материалом.
Что касается курса геометрии в идеологии РО, в настоящее
время он не разрабатывается. Мы предлагаем воспользоваться
одной из существующих программ и соответствующим комплектом
учебно-методической литературы, по возможности, используя
формы проведения занятий, характерные для развивающего
обучения. Естественно, в разрабатываемом курсе алгебры
будут широко использоваться необходимые сведения из курса
геометрии.
Содержание учебных блоков в 7 классе
(второй проход).
1. Повторение. Введение
в алгебру (20 часов).
Стартовая
работа по алгебре
Различные виды чисел и действия с ними (включая числовую
прямую). Решение текстовых задач. Решение линейных уравнений.
Выражения, числовые подстановки. Степени с натуральным
показателем. Простейшие преобразования (раскрытие скобок,
вынесение за скобки, приведение подобных членов).
Виды математических моделей для описания задач (алгебраические,
геометрические, схемы, таблицы). Соответствующие языки.
Переход от одного вида моделей к другим. Законы арифметических
действий, их обоснование с помощью геометрических моделей.
Преимущества и недостатки каждого вида моделей.
Факультатив . Перенос законов на все виды чисел, элементы
абстрактной алгебры.
2. Линейные неравенства с одной переменной (10 часов).
Неравенства. Числовая прямая как средство графического
моделирования неравенств. Представление о соответствии
между множеством действительных чисел и множеством точек
числовой прямой. Алгебраическое описание различных множеств
точек на прямой. Числовые промежутки. Основные свойства
неравенств. Решение линейных неравенств, их систем (и
совокупностей).
Простейшие неравенства с модулями, сводящиеся к системам
или совокупностям линейных неравенств.
Факультатив. Числовые множества.
Задачник
по теме "Линейные неравенства"
3. Координатная плоскость (10 часов).
Координатная плоскость. Координатный метод. Возможности,
которые он предоставляет: а) описание множеств точек на
плоскости алгебраическим языком (уравнения, неравенства);
б) графическое изображение уравнений, неравенств с двумя
переменными. Равносильность уравнений и неравенств. Уравнение
прямой. Объединение и пересечение точечных множеств на
координатной плоскости. Алгебраическое описание отрезков.
Системы и совокупности уравнений и неравенств с двумя
переменными. Системы линейных уравнений. Графический способ
их решения.
Факультатив. Многомерные пространства. Системы линейных
уравнений с несколькими переменными.
4. Выражения. Подстановка (15 часов).
Выражения и формулы. Числовые выражения. Строение выражений.
Порядок действий. Вид (структура) числового выражения.
Выражения с переменными. Переменная как место (пустое)
объекта в программе. Вхождения переменных в выражения.
Константы. Обозначение переменных буквами. Подстановки.
ОДЗ. Фиктивные переменные. Преобразование выражений. Упрощение
выражений. Первичное представление о тождестве выражений.
Целые выражения, представление в виде произведения сумм
и в виде суммы произведений. Формулы сокращенного умножения.
Факультатив. Элементы абстрактной алгебры. Алгебра множеств.
5. Функции (15 часов).
Выражение как "машинка", преобразующая наборы
чисел, поступающие на вход, в числа на выходе (отображение).
Тождество выражений и тождественные преобразования. Комбинирование
(композиция) "машинок". Ограничение количества
входов (уравниванием входов, введением констант). Параметры.
Графики машинок с одним входом (выражений с одной переменной).
Функция как однозначное соответствие, ее график. Функциональная
символика. Функциональная интерпретация уравнений и неравенств
с одной переменной.
Функции как новый класс моделей реальных ситуаций. Область
определения. Область значений. Способы задания функции
и переходы между ними.
Кусочные функции. |х|, [х], {х}, sign x. Реальные процессы,
описываемые с помощью кусочных функций.
Четность, нечетность; возрастание, убывание; непрерывность.
Нахождение особых точек (точки пересечения графика с осями
координат, координат точек пересечения двух графиков.
Графическое решение уравнений и неравенств с одной переменной.
Преобразование f(x + m) + n (параллельный перенос графика
вдоль осей координат) и симметрия относительно осей координат.
Факультатив. Функции нескольких переменных и способы их
графического изображения. Нечисловые функции (отображения).
Сжатие-растяжение. Композиция функций. Обратные функции.
6. Прямая пропорциональная зависимость Линейная функция
(10 часов).
Прямая пропорциональная зависимость как модель равномерных
процессов. Формула и график прямой пропорциональной зависимости.
Угловой коэффициент, его влияние на расположение графика.
Решение основных задач, связанных с исследованием функций,
применительно к прямой пропорциональности и линейной функции.
7. Системы линейных уравнений (10 часов).
Системы линейных уравнений с двумя переменными. Задачи,
приводящие к системам уравнений. Алгебраические способы
решения систем линейных уравнений с двумя переменными
(подстановки, алгебраического сложения).
Факультатив. Решение систем линейных уравнений с несколькими
переменными.
Резерв (30 часов) .
На главную страницу
секции
Ориентировочное содержание
учебных блоков
в 8-9 классах
1.Алгебраические
дроби.
Рациональная дробь. Основное свойство дроби, сокращение
дробей, приведение к общему знаменателю. Сложение, вычитание,
умножение и деление дробей. Совместные действия над дробями.
Преобразование рациональных выражений. Допустимые значения
переменных, область определения рационального выражения.
Упрощение рациональных выражений. Обратно пропорциональные
переменные, функция , ее график.
2. Квадратичная функция.
Функции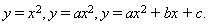 
Разложение квадратного трехчлена на множители. Квадратное
уравнение. Графическое решение квадратных уравнений. Специальные
типы квадратных уравнений. Выделение полного квадрата.
Формулы корней квадратного уравнения. Теорема Виета. Целые
корни квадратных уравнений, дробные корни квадратных уравнений.
Биквадратное уравнение. Распадающееся уравнение. Уравнение,
одна часть которого алгебраическая дробь, а другая равна
0. Решение текстовых задач с помощью квадратных уравнений.
Решение рациональных уравнений. Решение задач, приводящих
к рациональным уравнениям. Дробные уравнения с одной переменной.
[Целые алгебраические уравнения, целые корни, схема Горнера.]
Решение уравнений третьей и четвертой степеней с одним
неизвестным с помощью разложения на множители и введения
вспомогательной переменной. Решение рациональных уравнений
заменой переменных. Конические сечения. [Решение уравнений
в целых числах.]
Решение простейших систем, содержащих уравнение второй
степени. Уравнение окружности. Решение системы двух уравнений
с двумя переменными способом подстановки. Системы рациональных
уравнений, основные методы их решения: графический, подстановка,
алгебраическое сложение, введение новых переменных. Решение
систем, содержащих одно уравнение первой, а другое второй
степени. Решение систем двух уравнений с двумя переменными.
Решение задач методом составления систем.
Решение неравенств второй степени с одной переменной.
Решение квадратного неравенства с помощью графика квадратичной
функции. Решение рациональных неравенств методом интервалов.
Нестрогие рациональные неравенства. Решение систем рациональных
неравенств.
3. Действительные числа.
Натуральные числа и действия с ними. Делимость натуральных
чисел. Признаки делимости. [Алгоритм Евклида. Деление
с остатком целых чисел.] Обыкновенные дроби и десятичные
дроби. [Периодичность десятичного разложения обыкновенной
дроби.] Бесконечные периодические и непериодические десятичные
дроби. Рациональные числа, иррациональные числа. Понятие
об иррациональном числе. Положительные и отрицательные
числа. Общие сведения о действительных числах. Действительные
числа, их сравнение, основные свойства. Числовая прямая.
Модуль действительного числа, его свойства. Множества
чисел. [Множества. Комплексные числа.]
Измерение величин. Длина отрезка. Приближенные вычисления.
Приближенные значения величин. Погрешность приближения.
Относительная погрешность. Действия над приближенными
значениями. Применение свойств неравенств к оценке числового
выражения. Практические приемы приближенных вычислений.
[Приближения суммы и разности, произведения и частного,
суммы нескольких слагаемых. Приближенные вычисления с
калькулятором.]
Квадратный корень. Формула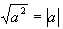
. Десятичные приближения квадратного корня. Простейшие
вычисления с калькулятором. Вычисления на калькуляторе
с использованием ячеек памяти. Вычисление на калькуляторе
степени числа и числа, обратного данному. Последовательное
выполнение нескольких операций на калькуляторе.
Решение задач на проценты. Отношения. Пропорции. Основное
свойство пропорций.
4. Степенная функция.
Функция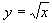 
и
ее график.[Представление об обратной функции.] Свойства
квадратных корней. Квадратный корень из степени, произведения
и дроби. Преобразования выражений содержащих квадратные
корни. Вынесение множителя из-под знака квадратного корня,
внесение под знак квадратного корня, действия с корнями.
Графическое решение уравнений вида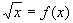
, где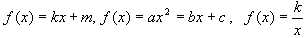
. Геометрическая интерпретация выражения |x - a| и использование
ее для решения уравнений вида |x - a| = r. Иррациональные
уравнения.
Свойства функции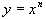
и ее график (отдельно случай n = 3). Степень с целым показателем
и ее свойства. Стандартный вид числа. Преобразование рациональных
выражений, записанных с помощью степени с целым показателем.
Корень n-ой степени. Корни четной и нечетной степеней.
Арифметический корень n-ой степени. Свойства арифметического
корня n-ой степени. Кубический корень. Корень n-ой степени
из натурального числа. Степень с рациональным показателем
и ее свойства. Функция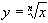
. Степенная функция. [Степень с действительным показателем.]
5. Числовые последовательности. Арифметическая и геометрическая
прогрессии.
Определение числовой последовательности и способы ее задания:
аналитический, словесный, рекуррентный. Монотонные последовательности.
Ограниченные и неограниченные последовательности. [Свойства
числовых последовательностей]. Арифметическая и геометрическая
прогрессии: определения, формулы n-го члена, формулы суммы
n членов, характеристические свойства. Бесконечно убывающая
геометрическая прогрессия, ее сумма. [Принцип полной индукции].
Простые и сложные проценты.
На главную страницу
секции
School
banner network
